工件载荷对机床定位误差的影响分析及补偿研究

文|南柯归洵

编辑|南柯归洵

影响机床加工精度的因素很多，如几何误差、热误差、切削力误差和刀具磨损误差等，除此之外，还有一些误差也同样值得研究，如机床上的工件和夹具的重量导致机床工作台受载所引起的误差，这一因素也是影响定位精度的重要原因之一，科学合理地测量和减小载荷产生的误差是减小机床整体几何误差的必要条件，因此，研究机床受载与机床几何误差之间的关系，同样具有重大的意义。

华中科技大学的Zhong等人通过对卧式机床装配平动轴的静力学分析，建立了机床基底、导轨和滑块以及工作台之间的误差传递模型，并且研究了机床主要零部件装备误差对机床空间几何误差的影响。

针对载荷对定位误差的具体影响及补偿等研究较少，载荷对定位误差影响的实际情况也同样重要，应引起足够的重视，以便为实际加工中的机床精度要求提供理论依据，在研究受载所引起的定位误差的同时，还需要选择科学合理地几何误差测量方法。

几何误差的测量方法可分为直接测量法和间接测量法，直接测量法是用相应的仪器直接测量单个几何误差，间接的空间位置测量不同的误差类型来直接获得对应的几何误差，选择适合的测量方法能够快速获得可靠的几何误差数据，并且有利于后续的误差补偿试验及研究。

图1

本文以VMC1000p三轴数控加工中心为例，通过测量数控机床受载前后的X轴的各项几何误差数据，并结合定位误差理论值的计算方法，提出了结合工件载荷的定位误差补偿方法，为减小工件载荷对数控加工机床精度的影响提供了理论指导。

由于机床零、部件本身及其装配过程中存在形状和位置误差，当机床运动部件移动或转动时，这些形状和位置误差会反映到机床的运动部件上，从而产生几何误差，在此次研究中，当机床工作台受到工件载荷时，其装配关系的细微变化以及机床丝杠运动时产生的误差均会反映到机床的定位误差上，因此，在试验中，以测量X轴定位误差为主要研究点，并观测了工件载荷对垂直度误差、直线度误差等的影响情况。

工作台与滑块的受载三维模型简图，如图1所示，其中将滚动导轨简化成四个滑块和导轨的组合，为方便设置描绘坐标系，现将工作台置于行程终点，它的体坐标系X₂Y₂Z₂-O₂和体参考坐标系X₁Y₁Z₂-O₂均设置在工作台参考平面的右上角，方向与机床坐标系的方向一致，如图2中的工作台受力简图所示。

图2

现假定工件w放置在工作台上任意位置，当工作台在行程起点时，其在体坐标系X₂Y₂Z₂-O₂和体参考坐标系X₁Y₁Z₁-O₂中的位置均为，(xw,yw,0)，当工作台沿X轴方向移动x时，即体坐标系X₂Y₂Z₂-O₂相对于体参考坐标系X₁Y₁Z₁-O₂沿X轴方向移动x。

故工件w在工作台体参考坐标系中的位置应是，(x1c+x,y1c,0)，z₂z₁o;9₁ₙ₂Xₙ₂k1,3wF2,1ha,.₂O₂′l→5x4i₂6ₙlₙl，O₂O₄₁₂X₁₂r₂x₃计算平面上两矢量：₁₂₂₁₁₁₂p₁₂=P₂−P₁=(l₁,0,△₁−△₂)₁₃₃₁₁₂₁₃p₁₃=P₃−P₁=(l₁,l₂,△₁−△₃)

根据这两矢量可求出平面的法向矢量n以及平面方程式5：n=p12⋯p23=|ijkl10Δ1−Δ2l1l2Δ1−Δ3|-l₂(Δ₁-Δ₂)(x₁-l₃-x)-l₁(Δ₂-Δ₃)·(y₁-l₄)+红(z₁+h+Δ₁)=0(5)

图3

由于不考虑工作台工件承载平面的变形，则可将₄₃ₙ₂₄₄P₄:(l₃+xₙl₂+l₄,−h−△₄)代入式5，可得△1=△2+△3=△4=010/式6即为滑块变形量的关系方程。

如下图3,假设在工作台参考坐标系X₁Y₂Z₂-O₂下工作台上表面任意点(ₓOₓ在该坐标系下的坐标为(x+xw,yw,0),则其对应的工作台下表面的点为(ₓOₓ′的坐标为，(x+xw,yw,−h)，在工件和工作台的自重作用下，ₓOₓ′点下移到Oxm,，距离为△z，则其在工作台参考坐标系X₁Y₁Z₂-O₂中的坐标，(x+xw,yw,−h+△z)。

显然，Oxm的坐标应满足式5，将点坐标代入，解得：Δz=(xw−ls)l1(Δ1−Δ2)+(yw−l4)l2(Δ2−Δ3)−Δ1(7)Oxn为在载荷作用下，工作台体坐标系的上表面任意点ₓOₓ产生方位变化后的新位置，o，与ₓOₓ″之间位置的水平变化为所求量△X(x);L1为P₁P₁线在平面x₁₀₁z₁的投影,空间直线P₁P₂的方程为x1−(l3+x)l1=y1−l40=z1+h+Δ1Δ1−Δ2(8)z₁Δst(x)9o₁A0;x₁6ₓOₓ′B400°setL₁△:图3工作台受载误差模型简图：

图4

在x₁o₁z₁面上的投影方程，即直线L₁的方程为：x1−(l3+x)l1=z1+h+Δ1Δ1−Δ2(9)从式9中可知此直线的斜率为：λ1=Δ1−Δ2l1则直线L₁与坐标系X₁Kz₂-O₂的O₁x₁轴的夹角为:Δ₁−Δ₂。

在x₁o₁z₁面上的投影方程，即直线L₁的方程为：x1−(l3+x)l1=z1+h+Δ1Δ1−Δ2(9)从式9中可知此直线的斜率为：λ1=Δ1−Δ2l1则直线L₁与坐标系X₁Y₂Z₂-O₂的O₁x₁轴的夹角为:△θ=arctan⁡△1−△2l1(10)。

由上述公式7和10可知,l₁,l₂,l₃,l₄为恒ₙxₙₙyₙ定量，xₙ和yₙ为已知的载荷位置，则工作台出现的下移和微倾仅与滚动导轨的形变有关，因而工作台下移和微倾产生的下移量Δz和倾斜角Δθ会引起X轴定位误差δX(x)产生改变，现定义，△z向上为正，Δθ逆时针为正，其中，倾斜角Δθ存在的顺时针和逆时针方向的倾斜会使定位误差，δX(x)出现减小和增大两种情况，如图5和图6所示:

图5

工作台受载后，若倾斜情况如图5所示，测量反射镜会向接近激光头方向偏移，使定位误差减小；

若倾斜情况如图6所示，测量反射镜会向远离激光头方向偏移，使定位误差增大，在实际运用中，还需要考虑工作台的厚度和工作台载体参考坐标系X₁Y₁Z₂-O；

图6

倾斜状态，由于与倾斜角Δθ和下移量Δz相关的变量Δ₁,Δ₂,Δ₃,Δ₄为滚动导轨方便受力计算所简化出的假设量，不具备实际测量价值。

因此，工作台的倾斜角Δθ和下移量△z直接由激光干涉仪和球杆仪获得，其中，角度Δθ为X-Z轴垂直度误差的变化量，由无载荷下的X-Z轴垂直度误差θ₁和加载荷下的X-Z轴垂直度误差θ₂获得；Δz为X轴沿Z轴方向的直线度误差的变化量，由无载荷下的X轴沿Z轴方向的直线度误差，δZ1(x)和加载荷下的X轴沿Z轴方向的直线度误差，δZ2(x)获得。

图7

结合图6中几何关系可得到待求量Δx(x)的理论值:Δx2(x)=AOxn→=AOxm→⋅tan⁡(△θ)=K⋅OxrOxm→⋅tan(△θ)(11)=K·△z·tan(Δθ)=K⋅(δz1(x)−δz2(x))⋅tan⁡(θ2−θ1)式中，系数K为.ₓₓₓₓ△BOₓ′Oₓ″∼△Oₓ″AOₓ″的相似比，即K=AOx→|OxOx→，由于工作台倾斜引起的垂直度误差与工作台的厚度和滑块的形变产生的垂直度误差相比都极小，因此，AOxm→可近似于ₓₓh,Oₓ′Oₓ′可近似于Δl，则K=(△l+h)/Δl。

通过对机床工作台施加载荷来模拟机床在实际加工过程中的工作状态，然后再借助激光干涉仪及相关的测量方法来获得机床的几何误差。

首先，设置对照组，分别是一组不施加载荷和一组施加100kg的载荷，并将其放置于工作台上偏向重心的同一位置，试验组中，选用100kg的载荷可以很好的模拟模具重量，也能够区分误差的产生是由工件载荷产生，而不是随机误差产生的。

然后，试验材料及仪器选用，试验对象：VMC1000p三轴立式加工中心，载荷选择：100kg标准砝码，几何误差测量仪器：激光干涉仪(用于测量轴的移动误差和转角误差)、球杆仪(用于测量轴与轴之间的垂直度误差)，仪器安装采集示意图如图7所示：

图8

由于工作台倾斜引起的垂直度误差与工作台的厚度和滑块的形变产生的垂直度误差相比都极小，因此，AOxm→可近似于ₓₓh,Oₓ′Oₓ′可近似于Δl，则K=(△l+h)/Δl，机床受载试验系统数控机床受载试验系统，通过对机床工作台施加载荷来模拟机床在实际加工过程中的工作状态，然后再借助激光干涉仪及相关的测量方法来获得机床的几何误差。

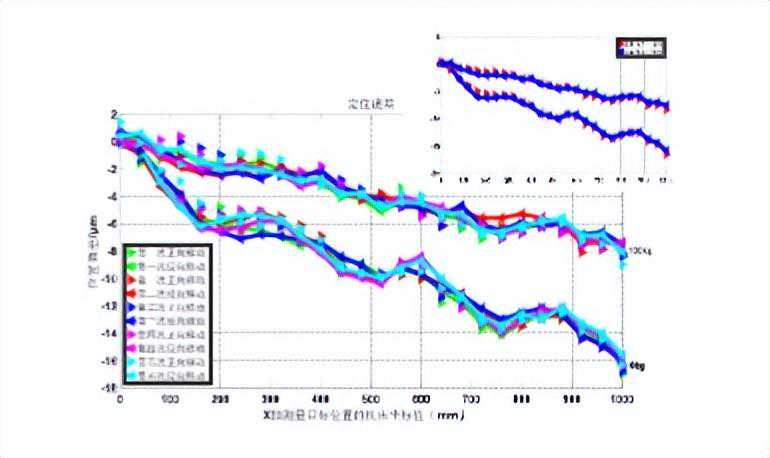
以采集的数控机床的几何数据为基础，研究了工件载荷对机床垂直度误差和直线度误差及定位误差的定位精度的影响，通过对比实际测量值，验证ₓₜ△ₓₜ(x)理论计算值是有效的。

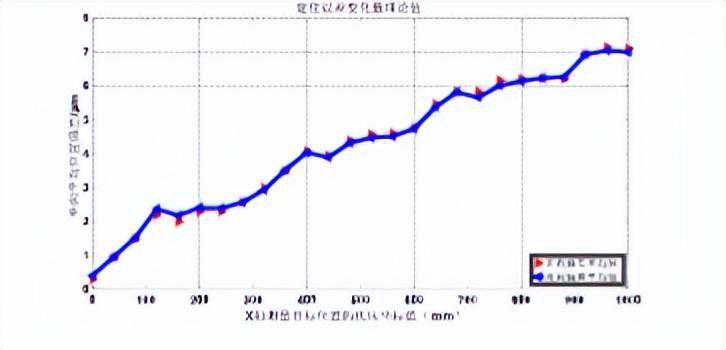
为了减小工件载荷对机床的精度影响，需要对受载机床进行螺距补偿。其考虑载荷和未考虑载荷的补偿结果如图9：

图9

上述数据表明，工件载荷对机床定位精度从未补偿前的15.5%扩大到补偿后的41.9%，即当机床定位精度越高时，工件载荷对其的影响也越明显。

同样地，考虑到100kg工件载荷的螺距误差补偿与未考虑到工件载荷的螺距误差补偿相比，机床的定位精度在未考虑载荷的基础上提升了41.9%。

该成果弥补了仅仅只做空载补偿所造成的欠量或过量误差补偿，考虑到工件载荷对机床影响后，这一情况得到了解决，使得机床的定位精度得到进一步的提升。

1)通过系统研究数控机床工作台的受载与定位误差之间的关系，分析出数控机床工作台在工件的载荷作用下受力是不均匀，这使得机床工作台会出现向左或向右两个方向上的倾斜，因此定位误差会出现增大或减少两种情况，其中，100kg的载荷对机床定位精度的影响在15%左右；

图10

2)结合九线几何误差辨识法计算出了定位误差理论变化量与实际测量出的定位误差测量变化量在图形上是吻合的，因此，数控机床工作台受载模型是有效的；

3)利用数控机床误差补偿单元可以减小工件载荷对定位误差的影响，其中，对100kg载荷的工件进行补偿后，定位精度比仅进行空载补偿时提升了41.9%。